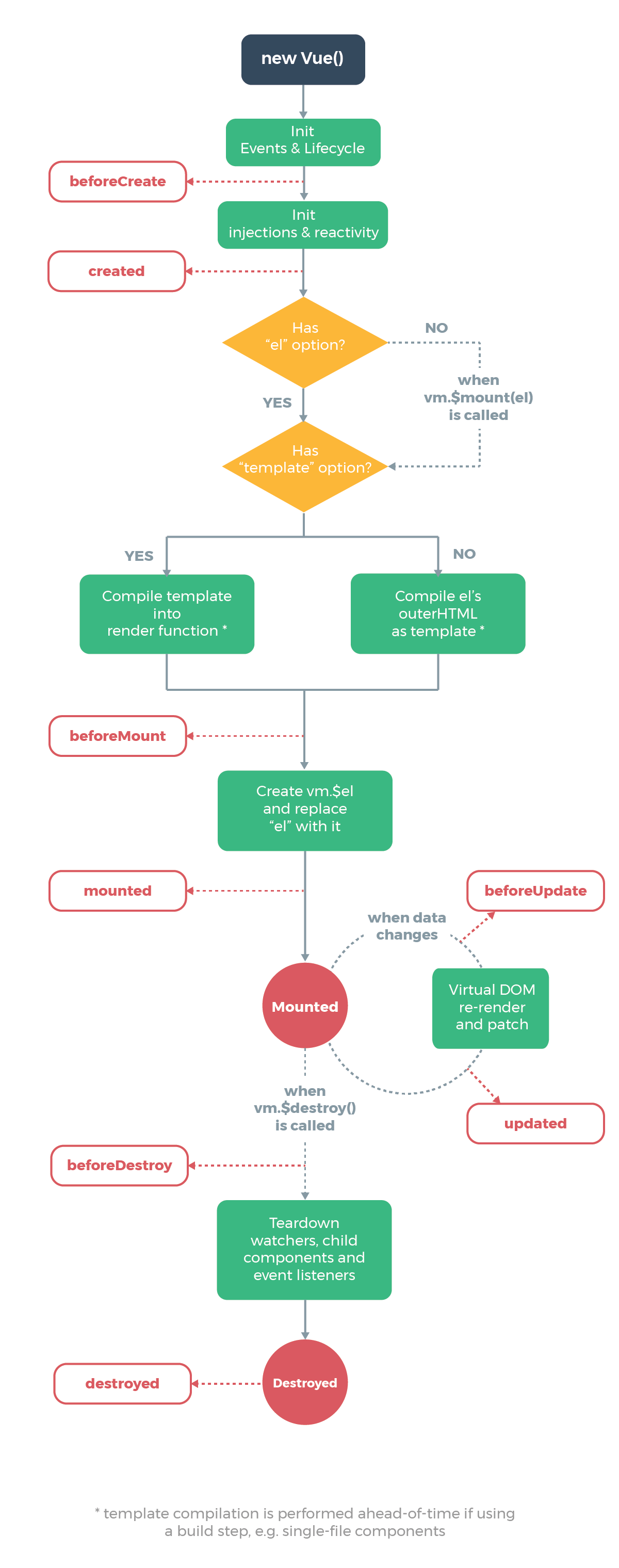
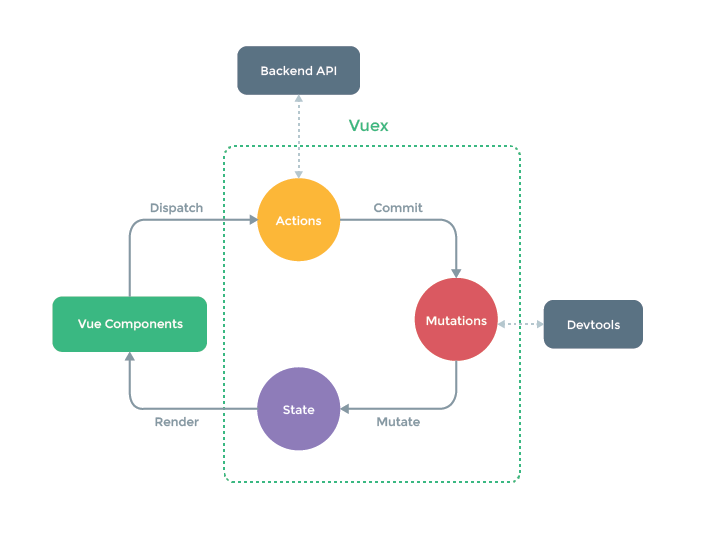
JavaScript目前发展很快,明年都会出一些新的语法特性。为了便于学习,本文对一些遇到的JavaScript语法特性做一些笔记。
JavaScript版本简介
JavaScript 由 Brendan Eich 于 1995 年发明,并于 1997 年成为 ECMA 标准。
ECMAScript 是该语言的官方名称。
从 2015 年起,ECMAScript 按年命名(ECMAScript 2015)。
| 版本 | 官方名称 | 描述 |
|---|---|---|
| 1 | ECMAScript 1 (1997) | 第一版。 |
| 2 | ECMAScript 2 (1998) | 只改变编辑方式。 |
| 3 | ECMAScript 3 (1999) | 添加了正则表达式。添加了 try/catch。 |
| 4 | ECMAScript 4 | 从未发布过。 |
| 5 | ECMAScript 5 (2009) | 添加了“严格模式”。添加了 JSON 支持。添加了 String.trim()。添加了 Array.isArray()。添加了数组迭代方法。 |
| 5.1 | ECMAScript 5.1 (2011) | 编辑改变。 |
| 6 | ECMAScript 2015 | 添加了 let 和 const。添加了默认参数值。添加了 Array.find()。添加了 Array.findIndex() |
| 7 | ECMAScript 2016 | 添加了指数运算符(**)。添加了 Array.prototype.includes。 |
| 8 | ECMAScript 2017 | 添加了字符串填充。添加了新的 Object 属性。添加了异步功能。添加了共享内存。 |
| 9 | ECMAScript 2018 | 添加了 rest / spread 属性。添加了异步迭代。添加了 Promise.finally()。增加 RegExp。 |
JavaScript新语法特性
…运算符
es6中引入扩展运算符(…),它用于把一个数组转化为用逗号分隔的参数序列,它常用在不定参数个数时的函数调用,数组合并等情形。
- 将实现了 Iterator 接口的对象转为数组
1 | var nodeList = document.querySelectorAll('div'); |
解构赋值
解构赋值语法是一种 Javascript 表达式。通过解构赋值, 可以将属性/值从对象/数组中取出,赋值给其他变量。
1 | let {a, b, ...rest} = {a: 10, b: 20, c: 30, d: 40} |
async函数
async函数是最新的javascript异步操作方式,初始定义于ES2017。async函数声明用于定义一个返回 AsyncFunction 对象的异步函数。异步函数是指通过事件循环异步执行的函数,它会通过一个隐式的 Promise 返回其结果。但是如果你的代码使用了异步函数,它的语法和结构会更像是标准的同步函数。
1 | /* 获取用户信息 */ |
ES6 class
请参考ES6篇 - class 基本语法和ES6-Class如何优雅的进行“糖化”。
参考链接
- JavaScript 版本,by w3school.
- ES6 扩展运算符 三个点(…),by ten5743.
- 解构赋值,by MDN web docs.
- async 函数的含义和用法,by 阮一峰.
- async function,by MDN web docs.
- 从面向对象设计角度,全面解读——JS中的函数与对象、Object与Function、以及原型链与继承,by scott.cgi.
- ES6篇 - class 基本语法,by 王锦添.
- ES6-Class如何优雅的进行“糖化”,by 前端小魔女.